47. ročník matematickej olympiády 1997-1998 | ||||
| Z4 | Z5 | Z6 | Z7 | Z8 |
| 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo |
| 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo |
| 3. kolo | ||||
Z4-I-1
Na prízemí 14-poschodového domu nastúpilo do výťahu 14 lenivcov. Každý z nich býva na inom poschodí. Výťah zastaví len raz. Na ktorom poschodí má výťah zastať, aby sa skupina čo najviac unavila, ak chôdza hore schodmi je 2-krát tak namáhavá, ako chôdza smerom nadol.
Z4-I-2
Keď škriatok Matík dopočítal príklad, všetky číslice sa mu rozutekali. Iba výsledok mu ostal. Trvalo mu veľmi dlho, kým ich prehovoril, aby sa vrátili. Len štvorky ho neposlúchli a poslali za seba iné číslice. A tak vznikol nesprávny príklad:
1080
5397
3936
9875
aký príklad mohol počítať Matík? Nájdi aspoň tri také príklady.
Z4-I-3
Traja súrodenci dostali od uja vrecúško guliek. Bolo tam 8 dúhových sklenených, 10 obyčajných sklenených a 9 hlinených. Jedna dúhová je rovnako cenná ako 5 obyčajných sklenených a jedna obyčajná sklenená je za 6 hlinených. Poraďte im, ako si majú guľky spravodlivo rozdeliť. Je viac možností?
Z4-I-4
Jeden kozmonaut bol vo vesmíre 169 dní, druhý bol ešte o 5 dní dlhšie. Napriek tomu bol prvý kozmonaut vo vesmíre o 1 nedeľu viac ako druhý. Ako je to možné?
Z4-I-5
Súťaže v streľbe zo vzduchovky sa zúčastnilo 6 pretekárov. Všetci dohromady získali 1035 bodov, pričom každý pretekár získal iný počet bodov. Víťaz nastrieľal o 5 bodov viac ako pretekár umiestnený na poslednom mieste. Koľko bodov získal tretí najlepší pretekár?
Z4-I-6
Ujo Mrkvička rýľoval záhradu tvaru obdĺžnika. Po dvoch hodinách prácu prerušil a išiel na obed. Ako dlho bude ešte musieť rýľovať po obede, ak mu ostal neporýľovaný záhon tvaru obdĺžnika s rozmermi 3-krát menšími ako má celá záhrada?
| ▲ hore ▲ |
Z4-II-1
Do 17 krúžkov, ktoré vidíte na obrázku, vpíšte celé čísla od l do 17 tak, aby súčet čísel v ľubovoľných troch krúžkoch ležiacich na jednej priamke bol 27.
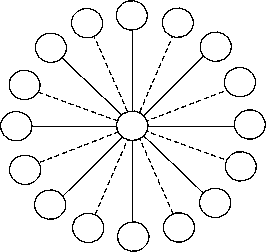
Z4-II-2
Ferko má 1125 tehličiek. Chce z nich postaviť múrik takéhoto tvaru:

Z koľkých tehličiek má postaviť spodný rad, aby na stavbu minul všetky tehličky?
Z4-II-3
Pozdĺž priamej cesty stojí 8 domov. Dva susedné sú vždy rovnako vzdialené od seba. Pred prvým domom stojí jedna, pred druhým dve, pred tretím tri, ..., pred ôsmym osem popolníc. Pred ktorým domom má zastať smetiarske auto, aby sa smetiari čo najmenej nachodili?
(Auto smie zastať len raz a smetiar naraz zoberie len jednu popolnicu!)
| ▲ hore ▲ |
Z5-I-1
Zistite, či sa môže stať, aby v roku nebol ani jeden piatok trinásteho.
Z5-I-2
Výpočet: 2097 + 6982 + 8339 = 17830 zrejme v poriadku nebude. Hela, Janka, Peter a Zuza sa rozhodli opraviť ho svojráznym spôsobom: Zamenili niektoré cifry v sčítancoch štvorkami tak, aby bol zápis pravdivý. Môže sa to každému z nich podariť zameniť iným spôsobom?
Z5-I-3
Emil chodí behať na futbalové ihrisko tvaru obdĺžnika s obvodom 300 m. Raz obiehal okolo celého ihriska, potom iba okolo jeho polovice tak, že si cestu pravidelne skracoval po stredovej čiare. Emil zistil, že obehne 12-krát celé ihrisko za rovnaký čas, ako 20-krát polovicu ihriska. Určte rozmery ihriska.
Z5-I-4
Na miske je 12 lieskovcov, 12 vlašských orechov a 23 paraorechov. Jeden vlašský orech stojí rovnako ako 7 lieskovcov. Jeden paraorech a 6 lieskovcov stojí spolu toľko čo 5 vlašských orechov. Rozdeľte oriešky na tri rovnako cenné kôpky. Nájdite dve rôzne rozdelenia.
Z5-I-5
Vierka zabudla v príklade
200 + 50 - 49 + 48 - 47 + 46 - ... - 5 + 4 - 3 + 2 - 1 =
s 51 číslami napísať ľavú a pravú zátvorku. Pamätala si len, že v zátvorkách bolo 20 čísel. Rozhodla sa, že urobí všetky možné umiestnenia takýchto zátvoriek a vo všetkých prípadoch príklady vypočíta. Aké výsledky bude mať Vierka po vypočítaní všetkých príkladov?
Z5-I-6
Myška našla 1.februára 1997 veľký syr v tvare kvádra a začala ho obhrýzať. Každý deň odhryzla rovnaké množstvo. Po mesiaci jej ešte zostal kváder s polovičnými rozmermi oproti pôvodnému kvádru. Koľko dní vydrží ešte myške tento syr?
| ▲ hore ▲ |
Z5-II-1
Maťo má dvoch súrodencov, staršiu sestru a mladšieho brata. Sestra sa narodila v máji roku 1987, brat v decembri 1994. Maťo sa narodil v utorok, prvé narodeniny oslávil v stredu, druhé v piatok. V januári ktorého roku sa narodil?
Z5-II-2
Obdĺžniky s rozmermi 2 a 3 cm, 4 a 5 cm a 8 a 7 cm sú poukladané vedľa seba tak, ako je nakreslené na obrázku. Určte obsah vyšrafovanej (vyfarbenej) časti.
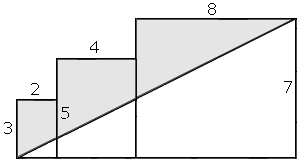
Z5-II-3
Ujo Ťažký mal problémy s hmotnosťou: vážil 117 kg. Lekár mu predpísal 2 červené a 3 žlté tabletky. Po červenej stratí štvrtinu hmotnosti, po užití žltej priberie 11 kg. V akom poradí má tabletky zjesť, aby vážil presne 94 kg, čo je jeho primeraná hmotnosť?
Pani Bláznivá vážila 53 kg a myslela si, že je tučná. Keď videla ako pán Ťažký po tabletkách schudol, kúpila si také isté a zjedla ich v rovnakom poradí ako on. Ako sa zmenila jej hmotnosť?
| ▲ hore ▲ |
Z6-I-1
Julka, Maťo, Veronika a Ondrík mali riešiť takúto úlohu:
Nahraďte niektoré cifry v číslach 2 891, 6 182 a 8 739 štvorkami tak, aby sa súčet rovnal 18 117. Je možné, aby mal každý z nich iné správne riešenie?
Z6-I-2
Kamil správne sčítal všetky štvorciferné čísla, ktoré pri delení siedmimi dávajú zvyšok 3 alebo 4. Petra správne sčítala všetky štvorciferné čísla, ktoré pri delení dávajú zvyšok 5 alebo 2. Kto z nich dostal väčší výsledok?
Z6-I-3
Na štvorčekovom papieri je narysovaný trojuholník ABC tak, ako ukazuje obrázok. Bodom C prechádzajú dve priamky štvorcovej siete (na obrázku vyznačené hrubšie). Nájdite na nich všetky také mrežové body M, aby priamka AM rozdelila trojuholník ABC na dva trojuholníky s rovnakým obsahom.
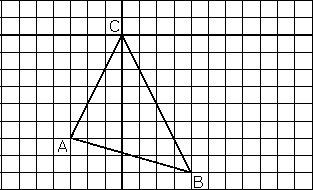
Z6-I-4
Dve švajčiarske známky sú rovnako cenné ako jedna francúzska, štyri talianske známky sú rovnako cenné ako sedem švajčiarskych. Svetlana má 7 francúzskych a 11 švajčiarskych známok. Ako ich má rozdeliť na tri kôpky rovnakej ceny? Nájdi všetky možnosti.
Z6-I-5
Myslím si číslo. Na číselnú os som znázornil jeho trojnásobok a sedemnásobok. Presne na takúto číselnú os znázornite (-6)-násobok mysleného čísla.
![]()
Z6-I-6
V päťuholníku ABCDE je |AB| = 2 cm, |BC| = 4,5 cm, |CD| = 12 cm, |DE| = 3,5 cm, |EA| = 5 cm. Zostrojte tento päťuholník, ak viete, že všetky jeho uhlopriečky obsahujúce bod A sú vyjadrené v centimetroch celými číslami. Nájdite všetky riešenia.
| ▲ hore ▲ |
Z6-II-1
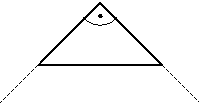 Mamička plietla šatku v tvare pravouhlého rovnoramenného trojuholníka. Začala pliesť od cípu s pravým uhlom. Po spotrebovaní jedného klbka zistila, že šatka je malá, lebo najdlhšia strana merala iba 57 cm. Mamička pokračovala v pletení, až kým nespotrebovala druhé, rovnako veľké klbko. Koľko merala potom kratšia strana šatky?
Mamička plietla šatku v tvare pravouhlého rovnoramenného trojuholníka. Začala pliesť od cípu s pravým uhlom. Po spotrebovaní jedného klbka zistila, že šatka je malá, lebo najdlhšia strana merala iba 57 cm. Mamička pokračovala v pletení, až kým nespotrebovala druhé, rovnako veľké klbko. Koľko merala potom kratšia strana šatky?
Z6-II-2
Členovia turistického klubu sa rozhodli ísť na výlet a vybrali si štyri rôzne trasy pochodu. Štvrtina všetkých členov klubu išla na sever, tri osminy všetkých členov klubu išli na východ a pätina všetkých členov klubu vyrazila na juh. Pre západný smer sa rozhodla desatina tých členov klubu, ktorí sa výletu zúčastnili. Desať členov na výlet nešlo a zostalo doma. Koľko členov má klub?
Z6-II-3
Digitálny budík ukazuje hodiny (napríklad: 13:47). Ako dlho na ňom v priebehu 24 hodín svieti aspoň jedna dvojka?
| ▲ hore ▲ |
Z7-I-1
Učiteľ napísal na tabuľu prirodzené číslo menšie ako 50 000.
Prvý žiak prehlásil, že to číslo je deliteľné dvoma
Druhý žiak prehlásil, že to číslo je deliteľné tromi.
Tretí žiak prehlásil, že to číslo je deliteľné štyrmi.
Takto to pokračovalo, až dvanásty žiak prehlásil, že to číslo je deliteľné trinástimi. Všetky tieto tvrdenia, okrem dvoch žiakov, čo hovorili za sebou, boli pravdivé. Aké číslo napísal učiteľ na tabuľu?
Z7-I-2
Kniha má viac ako 30 a menej ako 3000 strán. Všetky strany knihy sú očíslované. Na očíslovanie posledných listov knihy bolo potrebných 23 číslic. Koľko strán má kniha? Nájdite všetky možnosti.
Z7-I-3
Kristián zostrojil trojuholník ABC. Potom rozdelil uhly pri vrcholoch A a B na štyri rovnaké uhly. Pritom dostal tento obrázok. Zistil, že jeden z vyznačených uhlov je pravý. Vy zistite veľkosť uhla ACB.
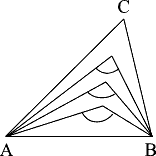
Z7-I-4
V zápise čísla 82 077 875 072 562 386 škrtnite niekoľko číslic tak, aby ste dostali čo najväčšie číslo deliteľné 36.
Z7-I-5
O trojuholníku ABC s najmenšou stranou dĺžky 1 cm sme dostali tieto informácie:
a) V trojuholníku ABC majú kružnica vpísaná a opísaná spoločný stred.
b) V trojuholníku ABC je súčet jedného z uhlov a polovičky druhého uhla rovný 90°.
c) V trojuholníku ABC platí, že ťažnice na strany AB a BC sú rovnako dlhé.
d) V trojuholníku ABC platí: |AB| = 2.|AC|.
Práve dve z týchto tvrdení sú pravdivé. Aký obvod môže mať trojuholník ABC? Zistite všetky možnosti.
Z7-I-6
Myslím si číslo. Na číselnej osi som okrem neho znázornil ešte aj číslo o 2 menšie a číslo 5-krát väčšie. Presne na takúto číselnú os znázornite číslo 1.
![]()
| ▲ hore ▲ |
Z7-II-1
Barón Prášil raz rozprával: "V začarovanej zemi stál čarovný stĺp. Keď ho človek obehol jedenkrát sprava, sám sa šesťkrát zväčšil. Keď ho obehol jedenkrát zľava, dvakrát sa zmenšil. Sám si to skúsil. Obehol som raz sprava a bol som šesťkrát väčší. Ale nikomu to nedoporučujem. Ani si neviete predstaviť, koľko som sa nabehal, aby som meral toľko, čo pôvodne, teda dva metre."
Hovoril barón Prášil pravdu?
Z7-II-2
Kráľ sa rozhodol, že Janka za dobré služby vyplatí dukátmi z pokladne. Povedal mu: "Môžeš si vziať buď najviac 30% dukátov z väčšej hromady, alebo najviac 70% dukátov z menšej hromady."
V pokladni je 113 dukátov. Rozdeľte ich na dve hromady tak, aby kráľ mohol vyplatiť Jankovi čo najmenej dukátov.
Z7-II-3
Sieť kvádra so štvorcovou podstavou P je vpísaná do obdĺžnika, ktorého dĺžky strán sú 69 cm a 84 cm (obrázok). Vypočítaj, aký môže byť objem tohoto kvádra.

| ▲ hore ▲ |
Z8-I-1
Rozhodnite, či sa dá štvorec rozdeliť na:
a) 1997,
b) 1998,
c) 1999
menších štvorcov. Svoju odpoveď zdôvodnite.
Z8-I-2
Anička a Zdenka mali odčítať dve kladné desatinné čísla. Anička omylom posunula v menšenci desatinnú čiarku o 1 miesto, čím dostala výsledok 13-krát menší ako bol správny výsledok. Zdenka omylom posunula v menšiteli desatinnú čiarku o 1 miesto, čím dostala výsledok o 14,58 menší ako bol správny výsledok. Zistite, aký bol správny výsledok.
Z8-I-3
Daný je deltoid ABCD s uhlami pri vrcholoch B, C, D po rade 90°, 135°, 90° a dĺžkou uhlopriečky |BD| = ![]() cm. Vypočítajte presne dĺžku uhlopriečky AC.
cm. Vypočítajte presne dĺžku uhlopriečky AC.
Z8-I-4
Zistite, či sa dajú všetky dvojciferné čísla rozdeliť do dvoch skupín tak, aby sa každé číslo nachádzalo práve v jednej skupine a aby sa súčiny všetkých dvojciferných čísel v každej skupine rovnali. Svoju odpoveď zdôvodnite.
Z8-I-5
Nech s, t sú reálne čísla. Na číselnej osi sú zľava doprava znázornené obrazy čísel s, t, 4t - 2s. Presne na takúto číselnú os znázornite číslo 5s + 13t.
![]()
Z8-I-6
Daný je rovnobežník ABCD. Nech K, L, M, N sú po rade ťažiská trojuholníkov ABD, ACB, BCD, DAC. Určte obvod rovnobežníka ABCD, ak obvod štvoruholníka KLMN je 84,48 m.
| ▲ hore ▲ |
Z8-II-1
Na Marse majú kalkulačky, ktoré majú len dve tlačidlá ![]() a
a ![]() , a displej, ktorý nezobrazuje číslice za desatinnou čiarkou. Keď stlačia tlačidlo
, a displej, ktorý nezobrazuje číslice za desatinnou čiarkou. Keď stlačia tlačidlo ![]() , číslo zobrazené na displeji sa vynásobí 4. Keď stlačia tlačidlo
, číslo zobrazené na displeji sa vynásobí 4. Keď stlačia tlačidlo ![]() , číslo zobrazené na displeji sa vydelí 5.
, číslo zobrazené na displeji sa vydelí 5.
Marťan Marťo stlačil tlačidlá v nasledovnom poradí: ![]() , a na displeji sa objavilo číslo 4. Aké číslo bolo na displeji na začiatku?
, a na displeji sa objavilo číslo 4. Aké číslo bolo na displeji na začiatku?
Z8-II-2
Miško našiel v bratovej učebnici takýto obrázok:
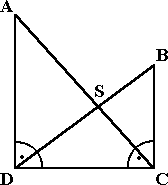 | |AD| = 9,6 cm |DC| = 2,4 cm |CB| = 3,2 cm |
Pod ním bol text: "Z uvedených dĺžok sa dajú vypočítať rozmery všetkých úsečiek v obrázku ..." Miškovi sa podarilo vypočítať dĺžky úsečiek DS, SB, a navyše vypočítal aj vzdialenosť bodu S od priamky DC, Aké boli jeho výsledky?
Z8-II-3
Pán učiteľ nadiktoval deťom dve desatinné čísla, ktorých rozdiel je 1,55. Deti ich mali sčítať a vynásobiť.
Janka v jednom čísle zle zapísala desatinnú časť - priamo za desatinnú čiarku omylom vpísala jednu nulu naviac. Ďalej počítala všetko s týmto pozmeneným číslom. Jej súčet bol o 0,63 menší než správny výsledok a jej súčin bol o 1,3545 menší než správny výsledok.
Aké čísla nadiktoval pán učiteľ deťom?
 Z8-II-4
Z8-II-4
Do štvorcovej siete 15 x 15 sme (po rade) napísali čísla od l do 225 tak, že v prvom riadku sú zľava doprava čísla od l do 15, v druhom riadku sú zľava doprava čísla od 16 do 30, ..., v pätnástom riadku sú zľava doprava čísla od 211 do 225. Kartičkou tvaru kríža (obrázok) zakrývame vždy 5 štvorcov siete. Nájdite všetky polohy kartičky, pri ktorých je súčet zakrytých čísel druhou mocninou prirodzeného čísla.
| ▲ hore ▲ |
Z8-III-1
V krajine Animálii sa nepoužívajú peniaze, ale pre obchodovanie existujú presné pravidlá. Podľa nich má 7 sliepok rovnakú hodnotu ako dve ovce, 2 kozy majú rovnakú hodnotu ako 1 prasa, 3 ovce majú rovnakú hodnotu ako 4 kozy, 5 prasiat má rovnakú hodnotu ako 3 býci. Môže pán Ryba v tejto krajine za svojho býka získať presne 3 zvieratá?
Z8-III-2
Do kružnice je vpísaný 5-uholník ABCDE, pre ktorý platí:
|Ð EAB| = 90° ,
|Ð ABC| = |Ð DEA| ,
|BC| = |CD| = |DE|
a obsah trojuholníka ABE je SABE = 4 cm2.
Určte obsah 5-uholníka ABCDE!
Z8-III-3
Nájdite všetky štvorice navzájom rôznych prirodzených čísel, ktorých súčet prevrátených hodnôt je rovný jednej.
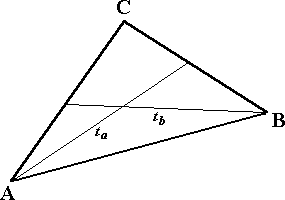
Z8-III-4
Trojuholník ABC je ťažnicou na stranu a a ťažnicou na stranu b rozdelený na tri trojuholníky a jeden štvoruholník (obrázok). Obsah štvoruholníka je 2 cm2. Vypočítajte obsah trojuholníka ABC!
| ▲ hore ▲ |