
| Z4 | Z5 | Z6 | Z7 | Z8 | Z9 |
| 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo |
| 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo |
| 3. kolo | |||||
Z4-I-1
Namiesto značiek doplň číslice tak, aby bol tento príklad správne vypočítaný.
 |
Z4-I-2
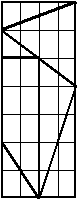
Škriatkovia Atramentík, Zemička, Jahôdka, Hrašuľko a Slniečko našli v lese zabudnutú
čokoládu. Rozlámali ju na kúsky tak, ako vidíte na obrázku, a pustili sa do nej.
Najväčší kúsok zjedol Hrašuľko. Slniečko a Atramentík zjedli rovnako veľa,
ibaže Slniečko tri kúsky a Atramentík len jeden. Zemička zjedol sedminu
čokolády a Jahôdka dojedol zvyšok. Pre každého trpaslíka vyfarbi jeho farbičkou
tú časť čokolády, ktorú zjedol.
Z4-I-3
Na obrázku vidíš kúsok číselnej osi. Doplň do obláčikov čísla, ak vieš:
Tri z dopĺňaných čísel sa dajú bezo zvyšku deliť 4.
Žiadne číslo nie je väčšie ako 111 ani menšie ako 94.
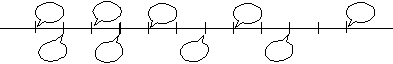 |
Z4-I-4
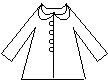 Mamička chce na Milkin kabátik prišiť 4 gombíky. Celkom má 5 žltých, 2 ružové a 1 modrý
gombík. Milka si želala, aby na zapínaní neboli vedľa seba dva gombíky tej istej farby,
a aspoň jeden z krajných gombíkov bol žltý. Koľkými rôznymi spôsobmi môže mamička
poprišívať gombíky, ak chce Milke vyhovieť? Nakresli všetky tieto kabátiky.
Mamička chce na Milkin kabátik prišiť 4 gombíky. Celkom má 5 žltých, 2 ružové a 1 modrý
gombík. Milka si želala, aby na zapínaní neboli vedľa seba dva gombíky tej istej farby,
a aspoň jeden z krajných gombíkov bol žltý. Koľkými rôznymi spôsobmi môže mamička
poprišívať gombíky, ak chce Milke vyhovieť? Nakresli všetky tieto kabátiky.
Z4-I-5
Na papieri sú znázornené body A, B, C, D, X a Y tak, že platí:
A, X, Y a D sú vrcholmi obdĺžnika.
X, B, C a Y sú vrcholmi obdĺžnika.
Štvoruholník ABCD má obsah 15 cm2.
Obdĺžnik AXYD má dvakrát väčší obsah ako obdĺžnik XBCY.
Úsečka AB meria 3 cm.
Vypočítaj obsah a obvod obdĺžnika AXYD.
Z4-I-6
Maťko má kartičky s číslicami 0, 1, 2, 3, 4, 5, 6, 7, 8 a 9. (Každú iba raz).
Z týchto kartičiek zložil tri trojciferné čísla. Prvé z nich má súčet cifier 13,
druhé 14 a tretie 15. Aký najmenší výsledok mohol Maťko dostať pri sčítaní týchto
troch čísel?
Z4-II-1
V záhrade rastú ruže, tulipány a klinčeky. Ruží spolu s tulipánmi je o 20 viac, ako tulipánov s klinčekmi. Tulipánov je o 5 viac ako klinčekov a ruží je 37. Koľko kvetov rastie v záhrade?
(Iné kvety ako ruže, tulipány a klinčeky tam nie sú.)
Z4-II-2
Na obrázku je kúsok číselnej osi. Práve tri z vyznačených bodov zodpovedajú trom za sebou
idúcim číslam deliteľným 4. Doplň chýbajúce čísla, ak vieš, že súčet všetkých dopĺňaných
párnych čísel je 660.
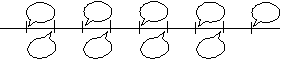 |
Z4-II-3
Na papieri sú znázornené body K, L, M, N, X a Y tak, že platí:
K, L, M a N sú vrcholy obdĺžnika.
X, L, M a Y sú vrcholy obdĺžnika.
Štvoruholník KLMN má obsah 32 cm2.
Obdĺžnik KXYN má o 4 cm väčší obvod ako obdĺžnik XLMY.
Úsečka KL meria 8 cm.
Vypočítajte obsah a obvod obdĺžnika XLMY.
Z5-I-1
Na Dračom ostrove žije 103 modrých a 113 zelených
drakov. Zlý čarodejník ostrov takto zaklial: Keď sa stretnú
traja draci jednej farby s piatimi drakmi druhej farby, tak všetci
ôsmi zmiznú. Je možné, aby na ostrove ostali len modrí draci?
Koľko by ich potom bolo?
Z5-I-2
Miško
sčítal dve čísla. Prvé z nich malo všetky číslice párne.
Druhé malo každú číslicu o jedna väčšiu ako číslo prvé
(t.j. keby na mieste stoviek v prvom čísle bola 4, v druhom by
bola na mieste stoviek 5). Súčet týchto dvoch čísel bol 9
163. Aké čísla Miško sčítal?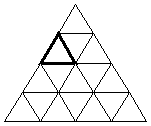
Z5-I-3
Ferdo mravec preliezal po mravenisku (obrázok).
Vieme, že išiel stále rovnako rýchlo a vyznačenú časť prešiel
za 6 sekúnd. Za akú najkratšiu dobu mohol prejsť všetkými
cestičkami mraveniska?
Z5-I-4
Odkedy sedemhlavý drak začal jesť ovsené vločky,
vzrástla ich spotreba v kráľovstve na dvojnásobok. Dnes už
ich zjedol 36 kilogramov, čo je denná spotreba pre tri jeho
hlavy. Aká je denná spotreba vločiek v kráľovstve? (Každá
hlava zje rovnako veľa vločiek)
Z5-I-5
Maťko išiel do obchodu. Na účtenke boli len
tieto čísla:
| 18,50 |
| 23,10 |
| 12,00 |
| 32,90 |
| 13,50 |
| 100,00 |
Kúpil 11 lízaniek, 9 žuvačiek, 7 perníkov, 3 nanuky a 1 čokoládu. Koľko stáli jednotlivé sladkosti?
Z5-I-6
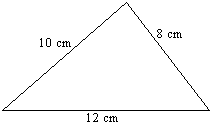
Aký najväčší a aký najmenší obvod môže mať
5-uholník zložený z troch trojuholníkov so stranami dĺžok
8 cm, 10 cm a 12 cm?
Z5-II-1
Keď ide Vilko do školy krokom, urobí 27 krokov. Keď do školy skáče, urobí 18 skokov.
Dnes si vymýšľa, striedavo robí 2 kroky vpred a jeden skok vzad, až kým sa nedostane
do školy.
Koľko musí urobiť krokov a koľko musí urobiť skokov, aby sa dnes dostal do školy?
 (Všetky kroky sú rovnako dlhé. Všetky skoky sú rovnako dlhé.)
(Všetky kroky sú rovnako dlhé. Všetky skoky sú rovnako dlhé.)
Z5-II-2
Koľko takýchto trojuholníkov potrebujeme na poskladanie 4-uholníka s obvodom 56 cm?
Nakresli všetky možnosti, ako taký 4-uholník môže vyzerať.
(Trojuholníky sa nesmú prekrývať.)
Z5-II-3
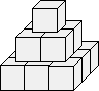
Na kockách v spodnej vrstve pyramídy na obrázku sú napísané rôzne prirodzené
párne čísla. Ich súčet je 100. Na každej inej kocke je napísaný súčet čísel kociek,
na ktorých táto kocka stojí. Aké najmenšie číslo môže byť na vrchnej kocke?
Z6-I-1
Päťciferné číslo má tieto vlastnosti:
druhá číslica sa rovná súčinu prvej číslice a prvej číslice,
štvrtá číslica sa rovná súčinu druhej a tretej číslice,
piata číslica sa rovná podielu druhej a štvrtej číslice.
Nájdi všetky také čísla.
Z6-I-2
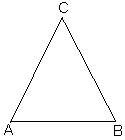
Napíš návod, ako sa len pomocou
kružidla presvedčiť, že trojuholník na obrázku je
rovnoramenný a veľkosť uhla ACB je 40°.
Z6-I-3
Dĺžky strán kvádra sú celé
čísla. Dve z jeho stien majú obsahy 147 cm2 a 539
cm2. Aký objem môže mať tento kváder?
Z6-I-4
V 6.A bol na polroku priemer známok
z fyziky 1,7. Na konci roka si Maťo zlepšil známku z 2 na 1,
Ivanka z 3 na 2 a Elenka zo 4 na 2. Paľko si známku zhoršil z
3 na 4. Priemer známok celej triedy sa takto zlepšil o 0,1. Koľko
najviac detí v 6.A mohlo mať na konci roka z fyziky jednotku?
Z6-I-5
Ak medzi číslice dvojciferného
čísla vsunieme číslo 51, dostaneme číslo deliteľné 7. Ak
tam vsunieme číslo 15, dostaneme číslo, ktoré pri delení
piatimi dáva zvyšok 2. Nájdi všetky dvojciferné čísla s
touto vlastnosťou.
Z6-I-6
Barón prášil narysoval niekoľko
konvexných mnohouholníkov. Tvrdil, že je medzi nimi aj štvoruholník
s troma ostrými uhlami, päťuholník a šesťuholník so štyrmi
ostrými uhlami. Koľkokrát mohol povedať pravdu? Vysvetli.
Z6-II-1
 Anička dostala krabičku lentiliek. Polovica z nich bola modrej alebo hnedej farby,
ostatné boli červené, žlté, prípadne zelené. Červených spolu so zelenými bolo o 12 viac,
ako žltých spolu so zelenými. Pritom červených bolo 19 a zelených bolo o 5 viac ako
žltých. Koľko lentiliek bolo v krabičke?
Anička dostala krabičku lentiliek. Polovica z nich bola modrej alebo hnedej farby,
ostatné boli červené, žlté, prípadne zelené. Červených spolu so zelenými bolo o 12 viac,
ako žltých spolu so zelenými. Pritom červených bolo 19 a zelených bolo o 5 viac ako
žltých. Koľko lentiliek bolo v krabičke?
Z6-II-2
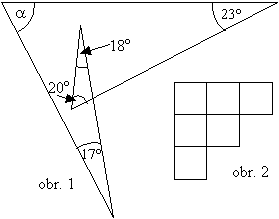
Vypočítaj veľkosť uhla α. (obr. 1)
Z6-II-2
Doplň do štvorčekov (obr. 2) čísla 1, 2, 3, 4, 5 a 6 tak,
aby súčet čísel v každom riadku bol 2-krát menší ako súčet čísel v riadku
tesne nad ním a súčty čísel v jednotlivých stĺpcoch boli 3 po sebe idúce čísla.
Nájdi všetky riešenia.
Z7-I-1
Lenka našla v knižke zaujímavú
postupnosť čísel. Každé číslo je ciferným súčtom súčinu
predchádzajúcich dvoch čísel. Prezradila nám, že na prvom
mieste tejto postupnosti je číslo osem, na treťom je
jednociferné číslo a na štvrtom je číslo 2. Aké číslo môže
byť na šiestom mieste tejto postupnosti?
Z7-I-2
Trojuholník ABC je
rovnoramenný. Jeho ramená AC a BC zvierajú uhol veľkosti 36°.
Os uhla CAB pretína stranu BC v bode D. Úsečka CD má dĺžku
8 cm. Akú dĺžku má strana AB?
Z7-I-3
V cukrárni predávajú 2
dl pomarančového džúsu po 12 Sk a 2 dl jabĺčkového po 8 Sk.
Okrem toho vám na požiadanie spravia aj miešaný jablkovo-pomarančový
džús, v ktorom sú jablková a pomarančová zložka zastúpené
v takom pomere, aby ceny oboch zložiek boli rovnaké. Koľko stojí 2 dl takéhoto džúsu?
(Za prípravu si neúčtujú nič.)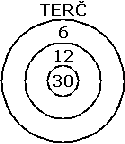
Z7-I-4
Vilko Tell strieľal na vyobrazený
terč. Nevystrelil viac, ako dvadsaťkrát. Každým šípom terč
zasiahol a priemerne získal na jeden zásah 17 bodov. Koľko
bodov mohol najviac získať?
Z7-I-5
Jedna zo strán oddĺžnika
ABCD je dvakrát kratšia, než jedna z uhlopriečok kosoštvorca
KLMN. Jedna zo strán kosoštvorca KLMN je rovnako dlhá jako
jedna z uhlopriečok obdĺžnika ABCD. Kosoštvorec KLMN má
obsah 36 cm2. Aký
obsah má obdĺžnik ABCD?
Z7-I-6
Starý pirát zanechal mapku ostrova s popisom cesty k pokladu:
“Z miesta označeného krížikom
sa pusti polovicu celkového počtu krokov na východ, potom urob
12 krokov na sever. Ďalej sa vydaj opäť na východ.
Urob tretinu krokov, ktoré ti chýbajú k pokladu. Zahni na
severovýchod a prejdi polovicu zvyšného
počtu krokov. Teraz ti ostáva urobiť 189 krokov na sever a
nakoniec 57 krokov na severozápad. Tam je zakopaný môj poklad.”
Koľko krokov treba prejsť od krížika až k pokladu?
Z7-II-1
Snehulienka kúpila 7 krabičiek syru Lunex. Keď
ich doma otvorila, zistila,že je síce v každej 180 gramov
syra, ale v niektorých je balený
takto: |
a v iných takto:
|
Môže Snehulienka rozdeliť syr medzi 7 trpaslíkov
tak, aby každý z nich mal rovnako veľa syra a
a) rovnaký počet "trojuholníčkov" syra?
b) najviac traja z nich mali rovnaký počet "trojuholníčkov" syra?
Z7-II-2
V školskej jedálni bola dnes na obed paradajková polievka. 40%
detí ju nemá rado, a preto ju vôbec nejedlo. Štvrtina detí
ju naopak veľmi obľubuje, a preto si dala dvojnásobnú porciu.
Zvyšné deti si zjedli každé svoj diel a v hrnci ostalo ešte
21 detských porcií. Pre koľko detí varili obed?
Z7-II-3
Na koľko vrstiev tvaru kvádra so štvorcovou podstavou musíme
rozrezať kocku, aby súčet povrchov jednotlivých častí bol
rovný dvojnásobku povrchu pôvodnej kocky.
Z8-I-1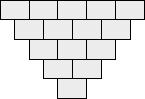
Vojto doplnil do
vrchného riadku tohoto sčítalkového trojuholníka (obrázok)
päť rôznych prvočísiel. Ich súčet bol 50. Aké najväčšie
číslo mu mohlo vyjsť "dole"?
Z8-I-2
Body A, B, C a D sú vrcholmi troch rôznych štvoruholníkov s obsahmi
9, 10 a 13 cm2. Aký obsah má zjednotenie týchto štvoruholníkov?
Zostrojte jednu takú štvoricu bodov.
Z8-I-3
Blcha so záujmom o matematiku lozila po učebnici a našla tam
číselnú os. Najprv sa po nej len slušne prechádzala, potom
začala skákať. Ale nie hocijako, preskakované čísla vždy
ležalo v strede jej skoku. Ako prvú preskočila -78. Z miesta,
kam dopadla, sa odrazila a preskočila -29, znovu sa odrazila a
preskočila 36. Na svoje veľké prekvapenie zistila, že dopadla
presne na to číslo, z ktorého začala skákať. Aké číslo
to bolo?
Z8-I-4
Majka našla v knihe zaujímavú postupnosť čísel. Všimla si,
že súčet troch po sebe idúcich čísel tejto postupnosti je vždy
20 alebo 22. Tieto výsledky sa pravidelne striedali: 20, 20, 22,
22, 20, 20, 22, ... . Na prvom mieste postupnosti bolo číslo 9,
na deviatom číslo 7. Aký je súčet prvých 100 čísel tejto
postupnosti?
Z8-I-5
Blcha sa dostala na štvorčekovú sieť so štvorčekmi
1 cm x 1 cm. Rozhodla sa že bude skákať po mrežových bodoch
tejto sieťky. Keďže jej šťastné číslo je 13, skáče vždy
len z bodu do bodu od neho vzdialeného 13 cm. Môže sa takto
dostať na ľubovoľný mrežový bod siete?
Z8-I-6
Tibor mal sčítať dve desatinné čísla väčšie jako 1. Nevšimol
si však ani jednu z desatinných čiarok a sčítal ich ako celé
čísla. Dostal tak výsledok 649. Správny súčet však mal byť
32,1*, číslicu na mieste stotín sme si nezapamätali. Aké
čísla mal Tbor sčítať?
Z8-II-1 Pyramída na obrázku je postavená z kociek očíslovaných prirodzenými číslami.
Žiadne dve kocky v spodnej vrstve nemajú rovnaké číslo. Číslo každej inej kocky
je rovné súčtu čísel 4 kociek, na ktorých táto kocka stojí. Zistite, aké najmenšie
číslo môže byť na hornej kocke, ak viete, že všetky kocky v prostrednej vrstve majú
rovnaké číslo.
Pyramída na obrázku je postavená z kociek očíslovaných prirodzenými číslami.
Žiadne dve kocky v spodnej vrstve nemajú rovnaké číslo. Číslo každej inej kocky
je rovné súčtu čísel 4 kociek, na ktorých táto kocka stojí. Zistite, aké najmenšie
číslo môže byť na hornej kocke, ak viete, že všetky kocky v prostrednej vrstve majú
rovnaké číslo.
Z8-II-2
Máme 4 rovnaké trojuholníky. Vieme z nich (bez prekrývania) poskladať nielen
obdĺžnik s obvodom 22 cm a obdĺžnik s obvodom 29 cm, ale aj kosoštvorec.
Aký obvod bude mať tento kosoštvorec? (Pri každom skladaní musíme použiť všetky
štyri trojuholníky.)
Z8-II-3
Súkromný podnikateľ prepustil štvrtinu svojich zamestnancov. Ich prácu
rozdelil medzi tých, ktorí ostali, každému z nich však zvýšil plat o 25 %.
Aj tak ale ušetril na mzdách 13 000 Sk. Zistite, koľko zamestnancov si ponechal,
ak viete, že všetci zarábajú (aj zarábali) rovnako, a to nie menej ako 6 tisíc a
nie viac ako 10 tisíc korún.
Z9-I-1
Zoberme si štvorciferné
číslo s rôznymi ciframi. Zameňme každú jeho číslicu
aritmetickým priemerom jeho zvyšných číslic. Aké najmenšie
a aké najväčšie číslo môžeme takto vytvoriť?
Z9-I-2
Uhlopriečka konvexného štvoruholníka
rozpoľuje úsečku spájajúcu stredy dvoch protiľahlých strán
tohto štvoruholníka. Dokážte,
že táto uhlopriečka delí štvoruholník
na dve časti s rovnakým obsahom.
Z9-I-3
Riešte sústavu rovníc:
x + y10 = 98,7 |
x10 je číslo x zaokrúhlené na desiatky, |
x10 - y = 23,4 |
y10 je číslo y zaokrúhlené na desiatky. |
Z9-I-4
Traja priatelia si
boli zaplávať v kruhovom jazere. Všetci skočili naraz do
vody z toho istého miesta. Julka plávala priamo na juh,
Vierka na východ a Stano rovno cez
stred jazera. Všetci doplávali
ku brehu v tom istom okamihu
a zistili, že ak by sa mali stretnúť
pri Vierke, prešli by všetci spolu po brehu o štvrtinu
dlhšiu trasu, ako keby sa stretli pri Julke. Ktorý z kamarátov
plával najpomalšie? Ktoré miesto je pre ich stretnutie najvýhodnejšie
(najmenej sa nachodia)? Narysuj trajektórie pohybu detí.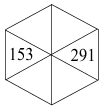
Z9-I-5
Doplňte do jednotlivých trojuholníkov
na obrázku celé čísla tak, aby sa v každom lichobežníku tvorenom tromi trojuholníkmi
súčet niektorých dvoch rovnal tretiemu.
Z9-I-6
Monika si na číselnej
osi zvolila číslo. Potom na nej vyznačila ešte ďalšie dve.
Jedno bolo 5-násobkom zvoleného čísla, druhé bolo o 5 väčšie
ako zvolené číslo. Dostala tak body A, B a C, pre ktorých
vzdialenosti platí: |AB| = 8 cm a |BC| = 6 cm. Ktoré číslo zvolila Monika na číselnej
osi?
Z9-II-1
V školskej jedálni boli dnes na obed parené buchty.
Každá učiteľská porcia je "šesťbuchtová", žiacka "štvorbuchtová.
Každý učiteľ zjedol celú svoju porciu, každé dievča zjedlo iba 3 buchty.
Tie, ktoré im zostali, dali chlapcom. Takže každý chlapec mal aspoň 5 buchiet,
trinásti dokonca 6. Spolu sa zjedlo 1386 buchiet, z čoho presne jednu jedenástinu
zjedli učitelia. Zistite, koľko dievčat, koľko chlapcov a koľko učiteľov dnes
obedovalo v školskej jedálni.
Z9-II-2
Daný je rovnostranný trojuholník ABC. Pätu výšky na stranu AB označíme M.
Os uhla CAB pretína stranu BC v bode K.
Priesečník priamok AK a CM označíme S. Bod P je stred úsečky AS
a bod Q je stred úsečky BS.
a) Dokážte, že štvoruholník PMQK je rovnoramenný lichobežník.
b) Vypočítajte dĺžky strán lichobežníka PMQK, ak viete, že obsah trojuholníka
ABC je ![]() cm2.
cm2.
Z9-II-3
Kváder s celočíselnými rozmermi sme bezo zvyšku rozrezali na dva trojboké hranoly.
Steny týchto hranolov majú obsahy 30 cm2, 35 cm2, 84 cm2,
91 cm2. Určte rozmery kvádra.
Z9-II-4
Nájdite také prirodzené číslo n, pre ktoré zároveň platí:
Zlomok ![]() sa dá napísať ako zmiešané číslo
sa dá napísať ako zmiešané číslo ![]() .
.
Zlomok ![]() sa dá napísať ako zmiešané číslo
sa dá napísať ako zmiešané číslo ![]() .
.
a + c = 105
b + d = 34

Z9-III-1
Na obrázku je nakreslená "skoromagická" vreckovka. Je čierno-biela,
pričom čiernu časť tvoria štvorce a bielu časť tvoria obdĺžniky.
Keby mali biela a čierna časť rovnaký obsah, bola by vreckovka magická.
Aké rozmery má magická vreckovka, ktorej
a) vnútorný štvorec má obsah 324 cm2?
b) rohový štvorec má obsah 16 cm2?
Z9-III-2
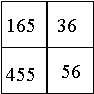
 Pyramída na obrázku je postavená z kociek očíslovaných prirodzenými číslami.
Žiadne dve kocky v spodnej vrstve nemajú rovnaké číslo.
Číslo každej inej kocky je rovné súčinu čísel 4 kociek, na ktorých táto kocka stojí.
Zistite čísla kociek v prvej a tretej vrstve, ak viete, že kocky v druhej vrstve sú
očíslované ako na obrázku.
Pyramída na obrázku je postavená z kociek očíslovaných prirodzenými číslami.
Žiadne dve kocky v spodnej vrstve nemajú rovnaké číslo.
Číslo každej inej kocky je rovné súčinu čísel 4 kociek, na ktorých táto kocka stojí.
Zistite čísla kociek v prvej a tretej vrstve, ak viete, že kocky v druhej vrstve sú
očíslované ako na obrázku.
Z9-III-3
Dve z hrán štvorstena majú dĺžky 2 cm a 6 cm. Zistite dĺžky zvyšných hrán
tohto štvorstena, ak viete, že všetky jeho steny majú rovnaký obvod a
najmenší možný obvod siete štvorstena je 18 cm.
Z9-III-4
Zistite, o koľko najviac percent (vzhľadom na svoju pôvodnú hodnotu) sa môže
zmeniť koreň rovnice
ax = b (a ≠ 0) s neznámou x,
ak žiaden z koeficientov tejto rovnice nezmeníme o viac ako 20 % jeho pôvodnej hodnoty.