54. ročník matematickej olympiády 2004-2005
| Z4 | Z5 | Z6 | Z7 | Z8 | Z9 |
| 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo | 1. kolo |
| 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo | 2. kolo |
| 3. kolo | |||||
Z4-I-1
Z čísla 6574839201 vyškrtni niektoré číslice tak, aby vzniknuté číslo bolo čo najmenšie a aby súčet cifier na mieste desiatok a mieste tisícok bol 7 a rozdiel cifier na mieste stoviek a mieste jednotiek bol 2.
Z4-I-2
Obdĺžnik JURO má obvod 36 cm, štvorec LENA má obvod 24 cm. JURO a LENA sú rodičmi obdĺžnikov a štvorcov, ktoré majú polovičný obvod ako LENA alebo polovičný obvod ako JURO. Pritom všetky dcéry sú štvorce a žiadny syn nie je štvorec. Koľko najviac môžu mať JURO a LENA rôznych synov a koľko rôznych dcér, ak rozmery detí sú v centimetroch zapísané celými číslami?
Z4-I-3
Stará mama plietla pre svoju vnučku Katku šál so vzorom s písmenami K. Najprv uplietla vzorku tvaru štvorca s dĺžkou strany 5 cm (pozri obrázok). Potom z takýchto vzorov urobila šál dlhý 1 m a široký 20 cm. Koľko bolo na šále písmeniek K?
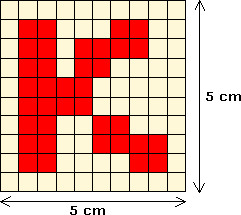
Z4-I-4
Od pondelka do piatku býva náš psík Bobi doma sám, lebo rodičia sú v práci a deti v škole. Jeden mesiac bol však sám iba 11 dní. Najprv bol tri dni od nedele do utorka doma Ivan, lebo ho bolelo brucho. Len čo vyzdravel, ostala doma Majka s chrípkou, a to od stredy do štvrtka ďalšieho týždňa. Koľko dní mohol mať ten mesiac?
Z4-I-5
Na Vianočných trhoch boli vystavené 5, 7 a 9 ramenné svietniky, pričom na každom ramene bola osadená jedna sviečka. Spolu tam bolo 9 svietnikov a 67 sviečok. Zisti, koľko ktorých svietnikov tam bolo.
Z4-I-6
Na telocviku bolo 9 chlapcov a 8 dievčat v dvoch zástupoch. V zástupe chlapcov bol každý chlapec o 1 cm vyšší než ten, ktorý stál tesne pred ním. V dievčenskom zástupe bolo každé dievča o 2 cm vyššie než to, ktoré stálo tesne pred ním. Najvyššie dievča bolo o 15 cm vyššie ako najnižší chlapec. Tretí najvyšší chlapec je Jurko a meria 134 cm. Koľko cm meria najnižšie dievča?
| ▲ hore ▲ |
Z4-II-1
Obdĺžnik VILO je dvakrát tak vysoký ako široký a jeho obvod je 24 cm. Deti VILA sú obdĺžniky (a štvorce) a majú polovičný obvod ako VILO. Jediný jeho syn zdedil po otcovi tú istú vlastnosť, že je dvakrát tak vysoký ako široký. Aké rozmery má syn? Aké rozmery môžu mať VILOVE dcéry, ak sú ich rozmery v centimetroch zapísané celými číslami a každá je iná?
Bodláková S.
Z4-II-2
Z čísla 8163452709 vyškrtni niektoré číslice tak, aby vzniknuté číslo bolo čo najmenšie a malo súčin cifier na mieste desiatok a mieste tisícok 24 a súčet cifier na mieste stoviek a mieste jednotiek 8.
Bodláková S.
Z4-II-3
Monika si v škole v prírode od pondelka až do soboty každý deň kupuje balíček cukríkov. Polovicu cukríkov z balíčka rozdá kamarátkam a dva zje sama. Ostatné odkladá sestričke Ivanke. V pondelok bolo v kúpenom balíčku 24, v utorok 16, v stredu 14, vo štvrtok 20 a v piatok 18 cukríkov. V sobotu ešte jeden balíček kúpila a ako vždy dala kamarátkam aj sebe. V nedeľu už cukríky nekupovala, ale počas cestovania domov polovicu ušetrených cukríkov s kamarátkami pojedli. Ivanke priniesla presne 20 cukríkov. Koľko bolo cukríkov v balíčku, ktorý kúpila v sobotu?
Dillingerová M.
| ▲ hore ▲ |
Z5-I-1
Viktor chcel napísať zoznam všetkých dvojciferných čísel, ktoré po delení piatimi dávajú zvyšok 3. Keď napísané čísla sčítal, dostal súčet 911. Ktoré číslo zabudol na zoznam napísať, ak tam žiadne nesprávne napísané nebolo?
Z5-I-2
Anička a Marienka mali mať zraz presne o 17:30 pred kinom. Anička si myslela, že jej idú hodinky o 4 minúty napred, ale v skutočnosti jej meškali 8 minút. Marienka si myslela, že jej hodinky 8 minút meškajú, ale išli jej o 4 minúty napred. Kedy ktoré z dievčat prišlo na zraz, ak si obe mysleli, že prišli presne o 17:30?
Z5-I-3
Traja princovia išli bojovať s mnohohlavým drakom. Najprv mu prvý princ ľavou rukou odsekol polovicu hláv a pravou rukou ešte ďalšie dve hlavy. Potom mu druhý princ tiež ľavou rukou odsekol polovicu zvyšných hláv a pravou rukou ešte ďalšie dve a napokon tretí princ mu ľavou rukou odsekol polovicu zvyšných hláv a pravou rukou ešte ďalšie dve. Potom drak padol bezhlavý na zem. Koľkohlavý drak to bol?
Z5-I-4 Na obrázku je mnohouholník zložený z 11 rovnakých štvorčekov. Zistite jeho obvod, ak jeden malý štvorček má obvod 20 cm. Ktoré dva štvorčeky mnohouholníka treba ubrať, aby vznikol nový mnohouholník s čo najväčším obvodom?
Na obrázku je mnohouholník zložený z 11 rovnakých štvorčekov. Zistite jeho obvod, ak jeden malý štvorček má obvod 20 cm. Ktoré dva štvorčeky mnohouholníka treba ubrať, aby vznikol nový mnohouholník s čo najväčším obvodom?
Z5-I-5
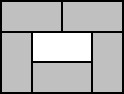
Hracia kocka má bodky rozmiestnené tak, že ich súčet na protiľahlých stenách je vždy 7. Kocka na obr. 2 stojí na stene s jednou bodkou, takže na podložke zanechá odtlačok "1". Keď prevalíme kocku doprava na stenu s dvomi bodkami, zanechá na podložke odtlačok "2". Keď potom prevalíme kocku smerom k sebe, zanechá odtlačok "3". Pri tomto prevaľovaní dostaneme stopu na obr. 3. Súčet čísel tejto stopy je 6.
Aký bude súčet na stope na obr. 4, ak východzie postavenie kocky je na obr. 2
Nakreslite, ako by mohla vypadať stopa, na ktorej je súčet 22, ak východzie postavenie kocky je na obr. 2?
 |  | |
| obr. 2 | obr. 3 | obr. 4 |
 Z5-I-6
Z5-I-6
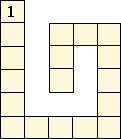
Ivanka si stavia zo stavebnice komíny. Všetky diely stavebnice sú rovnaké kvádre a majú rozmery 1 cm, 1 cm a 2 cm. Teraz postavila jednoposchodový dutý komín z piatich kvádrov na ploche 12 cm2 (viď obrázok). Rozhodla sa ale, že postaví dutý komín na ploche 36 cm2 z 260 takých kvádrov. Aký najvyšší komín mohla postaviť, ak jej žiaden kváder nezostal a komín bol na vrchu zarovnaný?
| ▲ hore ▲ |
Z5-II-1
Karol mal sčítať všetky dvojciferné čísla, ktoré po delení 10 dávajú zvyšok, ktorý sa dá bezo zvyšku deliť 5. Jedno z čísel však ale omylom zarátal trikrát, takže mu správnym sčitovaním vyšiel súčet 1035. Ktoré číslo zarátal tri razy?
Bednářová S.
Z5-II-2
Krtko si začal raziť nový tunel. Najprv vykopal 5 metrov na sever, potom 23 dm na západ, 150 cm na juh, 37 dm na západ, 620 cm na juh, 53 cm na východ a 27 dm na sever. Koľko centimetrov mu ešte ostáva vykopať, aby sa dostal na začiatok tunelu?
Dillingerová M.
Z5-II-3
Z čísla 9876543210 vyškrtni čo najmenší počet číslic tak, aby číslica na mieste desiatok bola číslo trikrát menšie ako číslo na mieste tisícok a číslica na mieste jednotiek bola číslo o tri menšie ako na mieste stoviek. Nájdi všetky riešenia.
Bodláková S.
| ▲ hore ▲ |
Z6-I-1
Desatinné číslo nazveme vyvážené, ak je súčet cifier nachádzajúcich sa pred desatinnou čiarkou rovný súčtu cifier za desatinnou čiarkou. Napr. číslo 25,133 je vyvážené. Napíšte
najväčšie,
najmenšie vyvážené číslo,
ktorého žiadne dve číslice nie sú rovnaké.
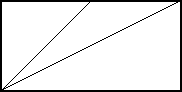
Z6-I-2
Obdĺžnik sme rozdelili na tri trojuholníky. V týchto trojuholníkoch sme správne odmerali všetky vnútorné uhly a získali sme tak tieto hodnoty: 20°, 30°, 30°, 40°, 50°, 60°, 90°, 90° a 130°. Dopíšte ich na správne miesta v nasledujúcom obrázku. (Pozor, obrázok môže byť veľmi nepresný, neoplatí sa merať!)
Z6-I-3
V krajine Čísielkovo žijú iba prirodzené čísla. Muži a chlapci sú párne čísla, ženy a dievčatá sú nepárne čísla. Manželia majú deti hneď po svadbe, a to všetky čísla, ktoré delia ich súčin bezo zvyšku. Ktorého nápadníka z čísel 2, 8, 14 si má vybrať slečna Sedmička, ak chce mať čo najviac rôznych detí? Ktorého nápadníka z čísel 2, 8, 14 si má vybrať slečna Sedmička, ak chce mať rovnako veľa synov ako dcér, ale žiadne dve deti rovnaké?
Z6-I-4
Na kartičke mám napísané párne štvorciferné číslo. Rozstrihnem ju tak, že získam dve dvojciferné čísla, ktorých súčin je 2562. Ktoré štvorciferné číslo som mala napísané na kartičke?
Z6-I-5 Na obrázku je mnohouholník zložený z 11 rovnakých štvorčekov.
Na obrázku je mnohouholník zložený z 11 rovnakých štvorčekov.
a) Zistite jeho obvod, ak viete, že jeden malý štvorček má obvod 2 cm.
b) Ktoré dva štvorčeky mnohouholníka treba premiestniť, aby vznikol nový mnohouholník s čo najväčším obvodom? (Ak sa premiestnený štvorec dotýka iného štvorca, musia mať spoločný buď iba vrchol alebo celú stranu.)
Z6-I-6
V Petroviciach, Bodríkovciach a Micinkove žije spolu 6000 obyvateľov. V každej z týchto troch dediniek pripadá v priemere na 20 obyvateľov 1 pes a na 30 obyvateľov 1 mačka. V Petroviciach a Bodríkovciach žije celkom 234 psov, v Bodríkovciach a Micinkove žije celkom 92 mačiek. Koľko obyvateľov majú jednotlivé dedinky?
| ▲ hore ▲ |
Z6-II-1
Desatinné číslo nazveme vyvážené, ak súčet jeho číslic ležiacich pred desatinnou čiarkou je rovný súčtu číslic za desatinnou čiarkou. Napr. číslo 25,133 je vyvážené.
V číslach 497365,198043 a 197352,598062 škrtnite niekoľko číslic tak, aby vzniklo
a) čo najväčšie vyvážené číslo,
b) vyvážené číslo s čo najväčším počtom číslic.
S. Bednářová
Z6-II-2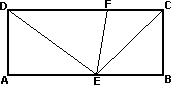 Obdĺžnik sme rozdelili na 4 trojuholníky tak, ako vidíte na obrázku. Presne sme odmerali veľkosti všetkých vnútorných uhlov. Získali sme tak hodnoty 15°, 20°, 20°, 50°, 55°, 70°, 75°, 75°, 90°, 90°, 130° a ešte jednu, ktorú sme zabudli zapísať.
Obdĺžnik sme rozdelili na 4 trojuholníky tak, ako vidíte na obrázku. Presne sme odmerali veľkosti všetkých vnútorných uhlov. Získali sme tak hodnoty 15°, 20°, 20°, 50°, 55°, 70°, 75°, 75°, 90°, 90°, 130° a ešte jednu, ktorú sme zabudli zapísať.
Zistite chýbajúcu veľkosť a napíšte, o veľkosť ktorého uhla sa jedná, ak viete, že úsečka DF je dlhšia ako FC. (Pozor, náš obrázok nie je presný, neoplatí sa merať!)
S. Bednářová
Z6-II-3
Keď v pekárni napečú buchty, rozdelia ich do balíčkov po 6 a po 12 kusoch. Z predaja 6-kusového balíčka majú zisk 4 Sk a z predaja 12-kusového balíčka 9 Sk. Koľko najviac a koľko najmenej buchiet môže byť na jednom pekáči, ak zisk z ich predaja je 219 Sk?
M. Dillingerová
| ▲ hore ▲ |
Z7-I-1
Dlhý, Široký a Bystrozraký si merali svoju výšku. Zistili, že Dlhý je dvakrát taký vysoký ako Široký. Bystrozrakého výška tvorí len dve tretiny výšky Dlhého, ale je o 44 cm vyšší ako Široký. Zistite, aký vysoký je Dlhý, Široký aj Bystrozraký.
Z7-I-2
Je dané päťciferné číslo deliteľné tromi. Ak z neho vyškrtneme číslice na nepárnych miestach, dostaneme dvojciferné číslo, ktoré je 67-krát menšie, než číslo získané z pôvodného päťciferného čísla vyškrtnutím číslic na párnych miestach. Zistite, aké mohlo byť pôvodné päťciferné číslo.
Z7-I-3
V krajine Čísielkovo žijú iba prirodzené čísla. Muži a chlapci sú párne čísla, ženy a dievčatá sú nepárne čísla. Manželia majú deti hneď po svadbe, a to všetky čísla, ktoré delia ich súčin bezo zvyšku.
a) Ktorého nápadníka z čísel 2, 16, 28, 46 si má vybrať slečna Deviatka ak chce mať čo najviac rôznych detí?
b) Ktorého nápadníka z čísel 2, 16, 28, 46 si má vybrať slečna Deviatka ak chce mať rovnako veľa synov ako dcér, ale žiadne dve deti rovnaké?
Z7-I-4
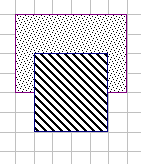
Kamilka pri kreslení obdĺžnikov (štvorec je špeciálny prípad obdĺžnika) v štvorcovej sieti narazila na takúto zaujímavú dvojicu: obdĺžnik s rozmermi 6 cm a 4 cm a štvorec so stranou dĺžky 4 cm. Najprv zakreslila do siete obdĺžnik a potom štvorec (pozri obrázok). S údivom vo svojom obrázku objavila, že obsah nezakrytej časti obdĺžnika je rovný obsahu štvorca a nezakrytá časť obvodu obdĺžnika sa rovná celému obvodu štvorca.
Medzi nasledujúcimi obdĺžnikmi nájdi všetky dvojice, ktoré majú obe vlastnosti Kamilkiných obdĺžnikov: 3 cm × 9 cm, 4 cm × 9 cm, 4 cm × 6 cm a 5 cm × 7 cm.
Z7-I-5
Myška Hryzka našla tehlu syra. Prvý deň zjedla ![]() syra, druhý deň
syra, druhý deň ![]() zvyšku, tretí deň
zvyšku, tretí deň ![]() zvyšku a štvrtý deň
zvyšku a štvrtý deň ![]() zvyšku syra. Potom už zo syra zostala iba kocka s povrchom 150 cm2. Aký objem mala pôvodná tehla syra?
zvyšku syra. Potom už zo syra zostala iba kocka s povrchom 150 cm2. Aký objem mala pôvodná tehla syra?
Z7-I-6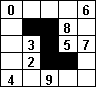 Archeológovia vykopali papyrus so zaujímavou tabuľkou s výrezom v tvare písmena Z (pozri obrázok). Domnievajú sa, že ide o talizman indiánskeho kmeňa Sčítačov. Každý ich talizman mal nasledujúcu vlastnosť: Ak v ňom zakrúžkujete ľubovoľných päť čísel tak, aby v každom stĺpci aj riadku bolo zakrúžkované práve jedno, a týchto päť čísel sčítate, dostanete vždy ten istý súčet. Pokúste sa zreštaurovať tento talizman, t. j. doplňte čísla na prázdne miesta.
Archeológovia vykopali papyrus so zaujímavou tabuľkou s výrezom v tvare písmena Z (pozri obrázok). Domnievajú sa, že ide o talizman indiánskeho kmeňa Sčítačov. Každý ich talizman mal nasledujúcu vlastnosť: Ak v ňom zakrúžkujete ľubovoľných päť čísel tak, aby v každom stĺpci aj riadku bolo zakrúžkované práve jedno, a týchto päť čísel sčítate, dostanete vždy ten istý súčet. Pokúste sa zreštaurovať tento talizman, t. j. doplňte čísla na prázdne miesta.
| ▲ hore ▲ |
Z7-II-1
V krajine Čísielkovo žijú iba prirodzené čísla. Muži a chlapci sú párne čísla a ženy a dievčatá sú nepárne čísla. Manželia majú deti hneď po svadbe a to všetky čísla, ktoré delia ich súčin bezo zvyšku. Pritom žiadne dve deti nemajú rovnakú hodnotu. Súčet hodnôt všetkých detí manželov Kvádrikových je 28. Otec Kvádrik má nižšiu hodnotu než aspoň jeden z jeho synov. Určte hodnoty pána a pani Kvádrikových.
M. Dillingerová
Z7-II-2
Koľko malých kociek, z ktorých každá má povrch 54 cm2, potrebujeme na postavenie plnej veľkej kocky s povrchom 864 cm2?
M. Krejčová
Z7-II-3
Máme štyri nádoby. V prvých troch je voda, štvrtá je prázdna. V druhej je dvakrát viac vody ako v prvej a v tretej je dvakrát viac vody ako v druhej. Do štvrtej nádoby prelejeme polovicu vody z prvej nádoby, tretinu vody z druhej nádoby a štvrtinu vody z tretej nádoby. V štvrtej nádobe sme takto získali 26 l vody. Koľko litrov vody je vo všetkých nádobách spolu?
M. Raabová
| ▲ hore ▲ |
Z8-I-1
Poradové číslo dňa v mesiaci je smutné, lebo v istom roku ani raz naň nepripadla nedeľa. Aké číslo to bolo a na ktorý deň v týždni pripadol v tom roku Nový rok?
Z8-I-2
Slimák liezol po štvorcovej sieti a zanechal za sebou stopu (pozri obr.1). Čísla pod stĺpcami a vedľa riadkov udávajú počet navštívených štvorčekov v danom stĺpci či riadku. Na obr. 2. dokreslite dráhu slimáka, ak viete, že nikdy nevliezol dvakrát do toho istého štvorčeka a že nikdy neliezol šikmo.
| obr. 1 | 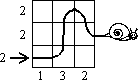 | 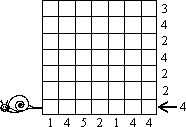 | obr. 2 |
Z8-I-3
O lichobežníku LICH so základňou LI vieme, že LC ^ HI, |Ð ILC|=|Ð IHC| a aritmetický priemer dĺžok jeho základní je 8 cm. Vypočítajte obsah tohto lichobežníka.
Z8-I-4
Koľko je medzi číslami 1, 2, 3, . . . , 999, 1 000 takých, ktoré nie sú deliteľné žiadnym z čísel 2, 3, 4, 5?
Z8-I-5 Alenka zostavovala "slimáčiu ulitu" z rovnoramenných pravouhlých trojuholníkov ako na obrázku. Použila na to čo najviac trojuholníkov, ale žiadne dva sa neprekrývali.
Alenka zostavovala "slimáčiu ulitu" z rovnoramenných pravouhlých trojuholníkov ako na obrázku. Použila na to čo najviac trojuholníkov, ale žiadne dva sa neprekrývali.
a) Z koľkých trojuholníkov bola ulita zostavená?
b) Vypočítajte obsah najväčšieho trojuholníka v hotovej ulite, ak odvesna najmenšieho z nich má dĺžku 1 cm?
Z8-I-6 Archeológovia vykopali papyrus so zaujímavou tabuľkou s výrezom v tvare písmena Z (pozri obrázok). Domnievajú sa, že ide o talizman indiánskeho kmeňa Sčítačov. Každý ich talizman mal nasledujúcu vlastnosť: Ak v ňom zakrúžkujete ľubovoľných päť čísel tak, aby v každom stĺpci aj riadku bolo zakrúžkované práve jedno, a týchto päť čísel sčítate, dostanete vždy ten istý súčet. Pokúste sa zreštaurovať tento talizman, t. j. doplňte čísla na prázdne miesta.
Archeológovia vykopali papyrus so zaujímavou tabuľkou s výrezom v tvare písmena Z (pozri obrázok). Domnievajú sa, že ide o talizman indiánskeho kmeňa Sčítačov. Každý ich talizman mal nasledujúcu vlastnosť: Ak v ňom zakrúžkujete ľubovoľných päť čísel tak, aby v každom stĺpci aj riadku bolo zakrúžkované práve jedno, a týchto päť čísel sčítate, dostanete vždy ten istý súčet. Pokúste sa zreštaurovať tento talizman, t. j. doplňte čísla na prázdne miesta.
| ▲ hore ▲ |
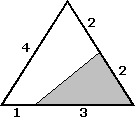
Z8-II-1
Daný je rovnostranný trojuholník so stranou dĺžky 4 cm (pozri obrázok). Určite obsah tmavej časti a koľko percent plochy pôvodného trojuholníka zaberá tmavá časť.
P. Tlustý
Z8-II-2
V domácej úlohe na výpočet hodnoty výrazu 2 - 3 + 4 - 5 + 6 - 7 + 8 - 9 + 10 si Rado zabudol zapísať dvoje zátvorky. Takže mu pri správnom počítaní vyšiel výsledok o 18 väčší, ako by získal, keby na zátvorky nezabudol. Doplňte dvomi rôznymi spôsobmi zátvorky a napíšte, aké číslo Radovi vyšlo a aké mu malo vyjsť.
M. Dillingerová
Z8-II-3
V priebehu prvých jedenásť dní odpovedalo na anketnú otázku 700 ľudí. Každý z nich si vybral práve jednu z troch ponúkaných možností. Pomer početnosti jednotlivých odpovedí bol 4:7:14. Dvanásty deň sa ankety zúčastnilo ešte niekoľko ľudí, čím sa pomer početnosti odpovedí zmenil na 6:9:16. Koľko najmenej ľudí muselo odpovedať na anketu dvanásty deň?
L. Šimůnek
| ▲ hore ▲ |
Z9-I-1
Dvojciferné číslo nazveme exkluzívne, ak má nasledujúcu vlastnosť: keď cifry exkluzívneho čísla navzájom vynásobíme a k tomuto súčinu pripočítame ciferný súčet daného exkluzívneho čísla, dostaneme práve toto exkluzívne číslo. Napríklad číslo 79 je exkluzívne, lebo 79 = 7 · 9 + (7 + 9). Nájdite všetky exkluzívne čísla.
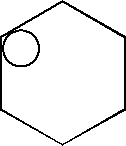
Z9-I-2
Vnútri pravidelného šesťuholníka so stranou dĺžky ![]() cm sa pohybuje kruh s priemerom dĺžky 1 cm tak, že sa stále dotýka obvodu pravidelného šesťuholníka. Vypočítajte obsah tej časti šesťuholníka, ktorá nemôže byť nikdy prekrytá pohybujúcim sa kruhom.
cm sa pohybuje kruh s priemerom dĺžky 1 cm tak, že sa stále dotýka obvodu pravidelného šesťuholníka. Vypočítajte obsah tej časti šesťuholníka, ktorá nemôže byť nikdy prekrytá pohybujúcim sa kruhom.
Z9-I-3
Koľko existuje spôsobov ako vybrať sedem čísel z množiny {1, 2, . . . , 8, 9} tak, aby ich súčet bol deliteľný tromi?
Z9-I-4
Nech sú dané kruh a štvorec s rovnakým obsahom. Do daného kruhu vpíšeme štvorec, do daného štvorca vpíšeme kruh. Ktorý z vpísaných obrazcov má väčší obsah?
Z9-I-5
Pán Párny mal párny počet ovečiek, pán Nepárny mal nepárny počet ovečiek. Počet všetkých ovečiek týchto dvoch pánov tvoril trojciferné číslo, ktoré malo všetky číslice rovnaké. Každej ovečke pána Párneho sa narodili tri ovečky, každej ovečke pána Nepárneho dve ovečky. Jedného dňa však vlk roztrhal tri ovečky pánovi Párnemu. Teraz má pán Párny rovnako veľa ovečiek, ako pán Nepárny. Koľko ovečiek mal pôvodne každý z chovateľov?
Z9-I-6
Päť detí postupne povedalo:
"Včera bol pondelok."
"Dnes je štvrtok."
"Pozajtra bude piatok."
"Zajtra bude sobota."
"Predvčerom bol utorok."
Keby ste vedeli, koľko detí klamalo, hneď by bolo jasné, ktorý je dnes deň. Ktorý je dnes deň?
| ▲ hore ▲ |
Z9-II-1
Princ Zrýchlený pozval princeznú Spomalenú na svoj hrad. Keď dlho nechodila, vydal sa jej naproti. Po dvoch dňoch putovania ju stretol v jednej pätine jej cesty. Spolu pokračovali v ceste už 2-krát tak rýchlo, ako keď cestovala princezná sama. Na princov hrad dorazili druhú sobotu od vzájomného stretnutia. Ktorý deň sa stretli, ak princezná zo svojho hradu vyrazila v piatok?
Dillingerová M.

Z9-II-2
Vnútri štvorca so stranou dĺžky 4 cm sa pohybuje kruh s priemerom dĺžky 1 cm tak, že sa stále dotýka obvodu štvorca. Vypočítaj obsah tej časti štvorca, ktorá nemôže byť nikdy prekrytá pohybujúcim sa kruhom.
Dillingerová M.
Z9-II-3
Do okresného kola súťaže postúpili Peter, Mojmír, Karol a Eva. V škole potom povedali:
Eva: "Z našej štvorice som nebola ani prvá ani posledná."
Mojmír: "Nebol som z našej štvorice posledný."
Karol: "Ja som bol z nás štyroch prvý."
Peter: "Ja som bol z našej štvorice posledný."
Vieme, že tri deti hovorili pravdu a jedno klamalo. Kto z nich bol v okresnom kole najlepší?
Volfová M.
Z9-II-4
Upratovačka umývala schodisko v mrakodrape. Aby jej práca lepšie ubiehala, počítala umyté schody. V dobe, keď mala umytých presne polovicu všetkých schodov, si urobila prestávku. Za chvíľu sa pustila znova do práce a chcela pokračovať v počítaní schodov. Keď si ale spomínala na počet už umytých schodov, dopustila sa omylu. Správne trojciferné číslo "prečítala" odzadu, čím vzniklo číslo menšie. Ďalej teda počítala schody od tohto menšieho čísla. Po umytí všetkých schodov došla k číslu 746. Koľko schodov mohla umyť v skutočnosti ak sa už viackrát nepomýlila?
Šimůnek L.
| ▲ hore ▲ |
Z9-III-1
Prirodzené dvojciferné číslo N strašne závidelo svojmu priateľovi, dvojcifernému desatinnému číslu x, jeho desatinnú čiarku. x malo dobré srdce, a tak mu tú svoju darovalo. N si ju celé šťastné vložilo medzi svoje dve číslice a vôbec mu nevadilo, že je teraz o 567 desatín menšie, ako bolo predtým. Aj x bolo spokojné, lebo teraz bolo na číselnej osi k svojmu priateľovi N dva razy bližšie, ako predtým. Zistite, o ktorých dvoch číslach N a x je táto príhoda.
S. Bednářová
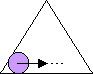
Z9-III-2
Vnútri rovnostranného trojuholníka so stranou dĺžky ![]() cm sa pohybuje kruh s priemerom dĺžky 1 cm tak, že sa stále dotýka obvodu trojuholníka. Vypočítaj obsah tej časti trojuholníka, ktorá nemôže byť nikdy prekrytá pohybujúcim sa kruhom.
cm sa pohybuje kruh s priemerom dĺžky 1 cm tak, že sa stále dotýka obvodu trojuholníka. Vypočítaj obsah tej časti trojuholníka, ktorá nemôže byť nikdy prekrytá pohybujúcim sa kruhom.
M. Dillingerová
Z9-III-3
Mamička pripravila na oslavu Jurkových narodenín pomarančový džús do džbánu tak, že zmiešala 1 liter 100%-ného džúsu s 2/3 litra 30%-ného džúsu. Jurko si odlial do pohára a ochutnal. Pretože má radšej slabšiu koncentráciu džúsu, dolial do pripraveného džbánu vodu do pôvodného množstva. Výsledný džús mal koncentráciu 61,2%. To už Jurkovi vyhovovalo. Aké množstvo džúsu si Jurko odlial do pohára?
M. Raabová
Z9-III-4
Je daný trojuholník. Ak jeho najdlhšiu stranu skrátime o tretinu jej dĺžky, najkratšiu zdvojnásobíme a poslednú zmenšíme o 2 cm, dostaneme trojuholník zhodný s pôvodným trojuholníkom. Zistite rozmery pôvodného trojuholníka.
M. Raabová
| ▲ hore ▲ |